Vấn Đề 8: SỰ TIẾP XÚC CỦA HAI ĐƯỜNG. TIẾP TUYẾN CỦA ĐưỜNG
CONG.
1. Ý nghĩa hình học của đạo hàm:
Đạo hàm của hàm số (C): y = f(x) tại điểm x0 là hệ số góc của tiếp tuyến với đồ thị (C) của hàm số tại điểm M0 (x0 ; f(x0)
Đạo hàm của hàm số (C): y = f(x) tại điểm x0 là hệ số góc của tiếp tuyến với đồ thị (C) của hàm số tại điểm M0 (x0 ; f(x0)
Khi đó phương trình tiếp
tuyến của (C) tại điểm M0 (x0 ; f(x0)
) là:
y – y0 = f ‘(x0).(x – x0) với: y0 = f(x0)
2. Điều kiện cần và đủ để hai đường (C1): y = f(x) và
(C2): y = g(x) tiếp xúc nhau là hệ phương
trình sau có nghiệm:
Nghiệm của hệ trên là
hoành độ tiếp điểm của hai đường
đó.
3. Nếu (C1): y = px + q và (C2): y = ax2 + bx
+ c thì (C1) và (C2) tiếp xúc nhau khi và chỉ khi phương trình ax2 + bx
+ c = px + q có nghiệm kép.
Dạng toán 1: Lập phương trinh tiếp
tuyến của đường cong (C): y = f(x)
Bai toán 1: Viết phương trinh tiếp tuyến
D của(C) : y = f (x) tại điểm M0 (x0 ; y0)
· Phương
trinh tiếp tuyến D có dạng : y −y0 = f '(x0 )(x
−x0 ).
- Nếu cho x0 thì tim y0 =
f (x0 )
- Nếu cho y0 thì tìm x0 là nghiệm của phương trinh f (x) = y0 .
- Tinh y ' =
f '(x) . Suy ra y '(x0 ) = f
'(x0 ) .
=> Phương
trinh tiếp tuyến D là: y −y0 = f '(x0 )(x
−x0 )
Bai toán 2: Viết phương trinh tiếp tuyến
D của (C) : y = f (x) biết D có hệ số goc k cho trước.
Cách 1: Tìm toạ độ tiếp điểm.
- Gọi M(x0; y0) là tiếp điểm. Tinh f' (x0).
- ∆ có hệ số goc k
⇒ f'(x0) = k (1)
- Giải phương trinh (1), tìm được x0 và tính y0 = f(x0).Từ đó viết phương trinh của D.
- Giải phương trinh (1), tìm được x0 và tính y0 = f(x0).Từ đó viết phương trinh của D.
Cách 2: Dùng điều kiện tiếp xuc.
- Phương trình đường thẳng D có dạng: y = kx + m.
- ∆ tiếp
xuc với (C) khi và chỉ khi hệ phương trinh sau có nghiệm:
=> Giải hệ (*), tìm được m. Từ đó viết
phương trinh của D.
Chú ý: Hệ số góc k của
tiếp tuyến D có thể được cho gián tiếp như sau:
- ∆ tạo
với chiều dương trục hoành góc a thì k = tana
- ∆ song
song với đường thẳng d: y = ax + b thì k = a
- ∆ vuông góc với đường thẳng d: y = ax + b
(a # 0) thì k = - 1/a
 - ∆ tạo
với đường thẳng d: y = ax + b một goc a thi :
- ∆ tạo
với đường thẳng d: y = ax + b một goc a thi :
Bai toán 3: Viết phương trinh tiếp tuyến
D của (C): y = f(x), biết D đi qua điểm A (xA ; yA )
Cách 1:Tim toạ độ tiếp điểm.
- Gọi M(x0; y0) là tiếp điểm. Khi đó: y0 =
f(x0), y’0 = f’ (x0).
- Phương
trình tiếp tuyến D tại M: y – y0 = f’(x0).(x – x0)
- D đi qua A (xA
; yA ) nên: yA – y0 = f'(x0).(xA – x0) (2)
=> Giải phương trinh (2), tìm được x0. Từ đó viết phương trình của D.
Cách 2: Dùng điều kiện tiếp xuc.
Phương trinh đường thẳng D đi qua A
(xA
; yA) có hệ số góc k: y – yA = k(x
– xA) D tiếp xúc với (C) khi và chỉ khi hệ phương trình sau có nghiệm:
=> Giải hệ (*), tìm được x (suy ra k). Từ đó viết phương trinh
tiếp tuyến D.














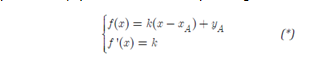


0 nhận xét:
Đăng nhận xét